テクノロジー・材料
ファインマンも解けなかった問題を解明 ~ファラデーの電磁誘導の法則とローレンツ力はなぜ同じ起電力を与えるのか~
筑波大学 計算科学研究センター小泉裕康准教授は、磁場を横切る導線に生じる誘導起電力が「ファラデーの電磁誘導の法則」と「ローレンツ力」という2つの本質的に異なる方法で求めることができるのはなぜかを明らかにしました。この誘導起電力を求める問題は高等学校の物理の教科書にも載っており、馴染み深い問題です。しかしそれにもかかわらず、2つの本質的に異なる方法で結果がなぜ一致するのか、これまで明らかにされていませんでした。
小泉准教授は、電子の運動を量子力学的な波動関数で記述すると同時に、電磁場をゲージ場とし、電場、磁場の代わりにゲージポテンシャルを用いることにより、この問題を解きました。その際、ゲージポテンシャルが持つゲージの自由度をエネルギー最小化という条件により固定しました。これにより、導線中の電子の量子状態を表す波動関数の位相因子に2重性があることが示されました。つまり、この位相因子が、1つの見方では電子の導線に沿った方向のローレンツ力による並進運動を表し、もう1つの見方では電場を生む時間依存したゲージポテンシャルと見なせることが示されました。このことから、古典電磁気学で見られた2つの本質的に異なる方法での奇妙な一致は、電子の量子状態を表す波動関数の位相因子の2重性により繋がっていた結果であることがわかりました。
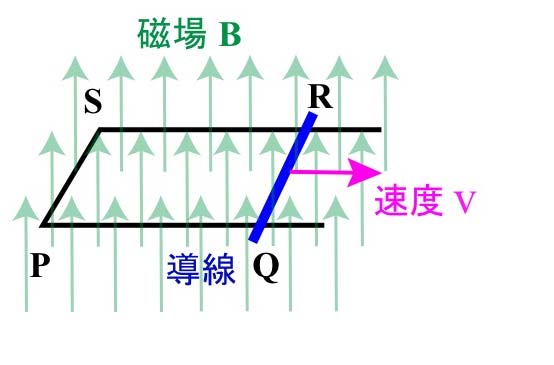
図 磁場B を速度v で横切る長さL の導線。誘導起電力BvL が回路PQRS に生じる。この誘導起電力はファラデーの電磁誘導の法則及びローレンツ力の2つの本質的にまったく異なる方法で計算できる。
小泉准教授は、電子の運動を量子力学的な波動関数で記述すると同時に、電磁場をゲージ場とし、電場、磁場の代わりにゲージポテンシャルを用いることにより、この問題を解きました。その際、ゲージポテンシャルが持つゲージの自由度をエネルギー最小化という条件により固定しました。これにより、導線中の電子の量子状態を表す波動関数の位相因子に2重性があることが示されました。つまり、この位相因子が、1つの見方では電子の導線に沿った方向のローレンツ力による並進運動を表し、もう1つの見方では電場を生む時間依存したゲージポテンシャルと見なせることが示されました。このことから、古典電磁気学で見られた2つの本質的に異なる方法での奇妙な一致は、電子の量子状態を表す波動関数の位相因子の2重性により繋がっていた結果であることがわかりました。

図 磁場B を速度v で横切る長さL の導線。誘導起電力BvL が回路PQRS に生じる。この誘導起電力はファラデーの電磁誘導の法則及びローレンツ力の2つの本質的にまったく異なる方法で計算できる。
